You can download SMTPlan with all benchmarks using the download link at the top. You can also view the benchmarks on GitHub here:
https://github.com/KCL-Planning/SMTPlan/tree/master/benchmarks
Results
Times in seconds for solving these problems with SMTPlan.
| Problem | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Nonlinear Car | 00.06 | 00.05 | 00.04 | 00.04 | 00.03 | 00.03 | 00.03 | 00.03 |
| Generator linear | 00.06 | 00.04 | 00.06 | 00.09 | 00.12 | 00.17 | 00.24 | 00.37 |
| Generator non-linear (Toricelli) | 00.06 | 00.09 | 00.10 | 00.17 | 00.39 | 01.01 | 02.36 | 05.87 |
Intel i5-6500U CPU @ 2.30GHz, 8GB RAM
PDDL+ benchmarks
Linear Generator
The generator domain is a PDDL+ benchmark problem that revolves around refueling a diesel-powered generator, which has to run for a given duration without overflowing or running dry.To test scalability the number of tanks is increased while decreasing the initial fuel level.
Non-linear Generator
This version of the generator domain uses a simplified non-linear equation to represent the effects of the refuel action. The fuel level in a refueling tank is calculated by:

where V init is the initial volume of fuel in the tank and t is the time spent refueling.
Generator (Toricelli)
This version uses the Torricelli’s Law, and hence the fuel level in a refuelling tank (Vfuel) is calculated by:
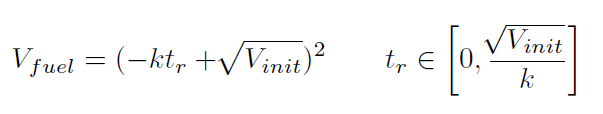
where V init is the initial volume of fuel in the tank, k is the fuel flow constant (which depends on gravity, size of the
drain hole, and the cross-section of the tank), and tr is the time of refueling (bounded by the fuel level and the flow
constant).
Here is an example of plan found by SMTPlan+ for the Torricelli nonlinear generator:
0.0: generate [1000.0]
959.0: refuel_tank1 [10.0]
959.0: refuel_tank2 [10.0]
Non-linear Car
The car domain is another PDDL+ benchmark (Fox and Long 2006). A vehicle has to cover a given distance and have a zero velocity at the end. The actions available are accelerate and decelerate, incrementing and decrementing the current acceleration by 1, respectively. The drag equation is removed from this problem, as currently z3 is unable to solve problems involving logarithms.
To test scalability, the bound on maximum acceleration/deceleration is increased.