L-RPG by KCL-Planning

An introduction.

L-RPG is a lifted planner that does not rely on grounding to solve planning instances, unlike most modern planners -- like FF and FastDownward -- that ground before planning starts. Not grounding is a dual-edged sword:

Pros:

We save a lot of memory which allows us to tackle larger problem instances.
The techniques we use allows us to calculate heuristics faster.

Cons:

We get weaker heuristic estimates.
There is an overhead to create successor states.

Indeed, planners that rely on fully grounding the domain can run out of memory during grounding! Some heuristics, like merge & shrink and pattern databases, bound the memory allowed. However, the construction of the data structures for these heuristics still requires grounding. Traditionally lifted heuristics have been very uninformative. For example, least-commitment Planners like UCPOP have used counting the number of open flaws or the number of open conditions as a heuristic estimate. L-RPG introduces an heuristic that is competitive with FF's RPG heuristic whilst not having to ground the entire domain.

Equivalent Objects

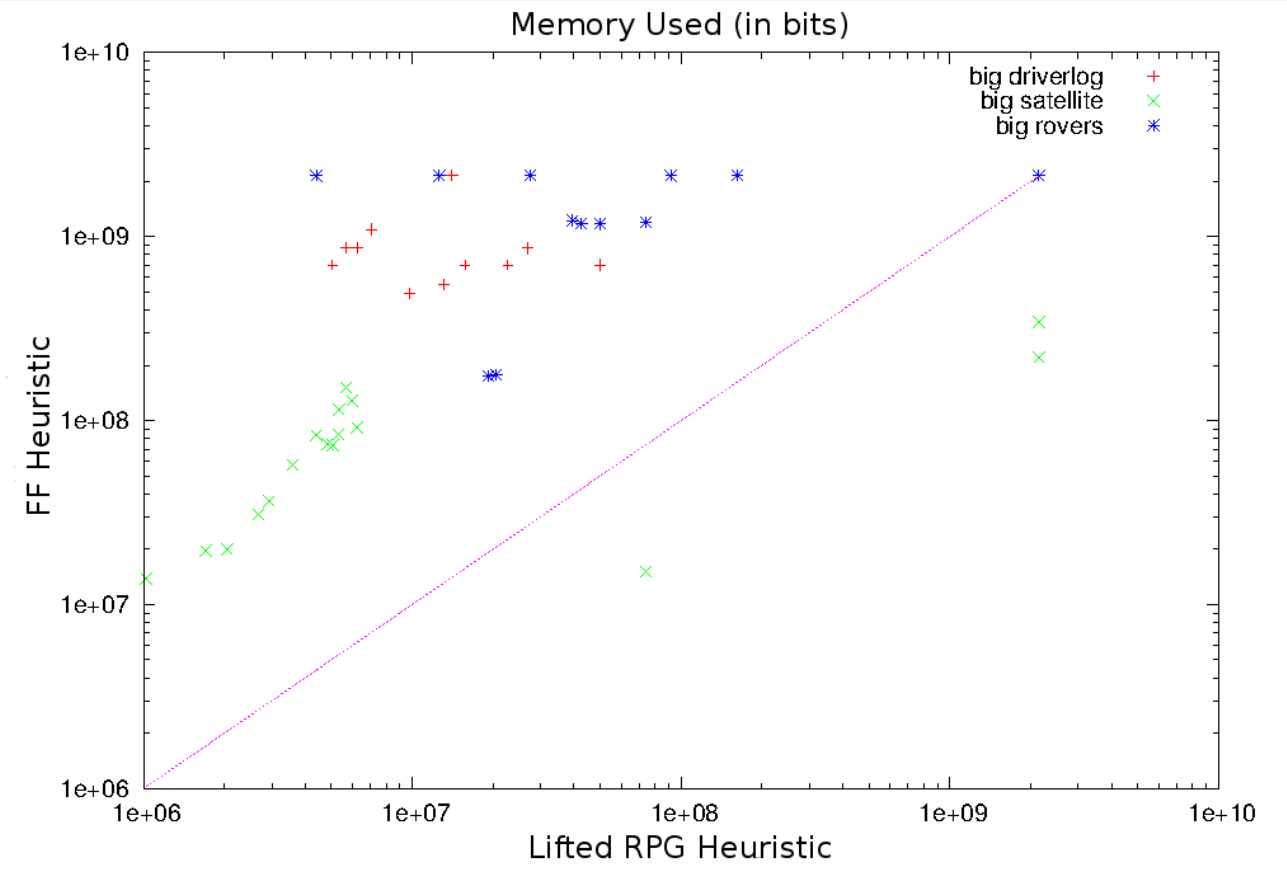
Consider the Driverlog problem instance depicted in Figure 1. The trucks t2 and t3 start at the same location, are empty, and are not being driven by a driver. It is clear that when constructing an Relaxed Planning Graph the same set of actions will be applied to all these trucks and that any fact that is reachable for one truck (e.g. (at t2 s3) ) will also be reachable for any of the other trucks (e.g. (at t3 s3) ). These trucks are equivalent, so we can substitute these instances with a new object T. This reduces the size of the RPG considerably because instead of dealing with these two trucks separately we now only need to consider one.

Just as the trucks in can be made equivalent, it is clear that although the instances of type driver – d1, d2, d3, and d4 – are not at the same location in the initial state they can become equivalent too. This is because all these drivers can reach the same locations and board the same trucks, any fact that is reachable for one driver is also reachable for the other drivers. Finding and exploiting these equivalence relationships between objects are key to L-RPG.

Figure 1: A simple Driverlog problem instanced. The dashed lines can be traversed by drivers and the solid lines can be traversed by trucks.

Details of how these equivalence relationships are found are in the paper. In general we use TIM to infer sets of objects that could become equivalent. These equivalence sets are then used during the construction of the RPG.

Constructing the RPG

To construct the RPG we used partially-grounded actions. Actions are grounded according to the equivalence sets found during the TIM analysis. For example, the following drive actions are created:

(drive {t1, t2, t3, t4} {s1} {s2})
(drive {t1, t2, t3, t4} {s2} {s1})

The trucks are part of the same equivalence set whilst the locations are not. We construct the RPG much like FF does with these partially-grounded actions. The key difference is that we check at each fact layer which objects have become equivalent and merge them. For example, t2 and t3 are equivalent in the initial fact layer and are merged into a single object. Similarly, after creating the second fact layer we can merge d1 and d2, because (1) They are part of the same equivalence set and; (2) Have reached each others initial state: (at d1 s1) and (at d2 p1), respectively. The constructed RPG is depicted in Figure 2.

Figure 2: The lifted RPG for the Driverlog problem, NOOPs have been omitted. T = {t1,t2,t3,t4}; D= {d1,d2,d3,d4}.

Calculating the heuristic

Given a constructed Lifted Relaxed Planning Graph (L-RPG) we extract a relaxed lifted plan much like FF. Unfortunately, this yields very poor heuristics, much like previous lifted heuristics. The reason is the merging of equivalent objects during the construction of the RPG. For example, if the goal is (driving d1 t2) then we can see in Figure 2 that this fact is achieved in the 2nd fact layer by applying the action (board {d1, d2, d3, d4} {t1, t2, t3, t4} s1), giving a heuristic estimate of 1.

The problem is that in the 2nd fact layer the drivers d1 and d2 become equivalent, this means that because d2 can board t2 so can t1. In short during the extraction of a relaxed plan from the L-RPG we substituted d1 for d2. To augment the heuristic we instantiate the applied action, which means we take the intersection of the variable domains of the action's parameters and the fact we want to achieve (in this case (driving d1 t2)). This gives us (board {d1} {t2} s1). Then we check its preconditions with the previous fact layer and see if any of the variable domains become empty. The fact (at t2 s1) is true in the initial fact layer, but (at d1 s1) is not.

We have experimented with two ways to augment the heuristic:

ObjectSub: Find the first layer where the objects (in this case d1 and d2) become equivalent and add that fact layer to the heuristic.
GoalSub: Add the violated precondition (in this case (at d1 s1)) as a new goal and find a relaxed plan to achieve it.

Further improvements

In addition we have created two more additions to L-RPG to improve it.

Preserve goals: We try to construct an L-RPG that does not include any actions that could delete any goals that have previous been achieved. If we cannot find a relaxed plan then we relax this constraint and rebuild the full L-RPG.
Helpful actions: Like FF we use helpful actions to prune the search space.

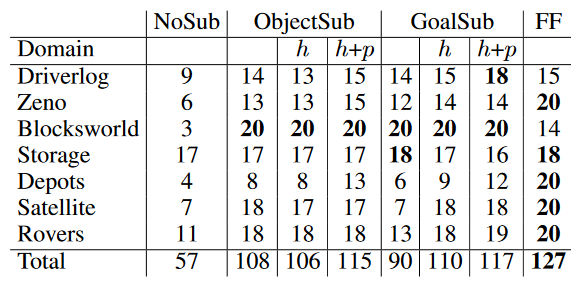
Results

The results of L-RPG compared to FF are depicted in Figure 3. As we can see the version that does not use any substitution performs very poorly. On the other hand the GoalSub with helpful actions and preservation of goals is very competitive and even outperforms FF on some domains.

Figure 3: Number of problems solved. h means helpful actions. p means that goals are preserved.

The memory results on larger problem instances is depicted in Figure 4. For these problem instances we added a lot more resources to the domain (rovers, satellites, drivers, and trucks). We see that our planner can solve large problem instances whereas FF dies whilst grounding.

Figure 4: Memory usage on large problem instances.